The "tema pitagoras" has fascinated mathematicians, educators, and enthusiasts for centuries, offering a timeless exploration into the harmony of numbers and geometry. Rooted in the teachings of the ancient Greek mathematician Pythagoras, this topic intertwines mathematics, philosophy, and even music in a way that remains relevant in modern times. Whether you're a student, a teacher, or simply someone curious about the foundations of math, the "tema pitagoras" provides a unique lens to view the world.
From its origins in ancient Greece to its application in contemporary mathematics, the "tema pitagoras" embodies the essence of logical reasoning and problem-solving. It serves as the backbone for various mathematical concepts, including algebra, trigonometry, and geometry. Beyond academics, its principles influence architecture, art, and even natural sciences. This article delves deep into the principles, historical significance, and real-world applications of the "tema pitagoras," making it an essential read for anyone looking to grasp the depth of this fascinating subject.
In this comprehensive guide, we will navigate through the biography of Pythagoras, examine the Pythagorean Theorem, and explore how its principles impact daily life and advanced mathematics. Along the way, we’ll answer key questions, address common misconceptions, and provide practical examples to solidify your understanding. Ready to unlock the mysteries of the "tema pitagoras"? Let's dive in!
Table of Contents
- Biography of Pythagoras
- What Is the Tema Pitagoras?
- Historical Significance of Tema Pitagoras
- Key Principles of the Pythagorean Theorem
- How Does the Pythagorean Theorem Work?
- Real-World Applications of Tema Pitagoras
- Tema Pitagoras in Modern Education
- Common Misconceptions About Tema Pitagoras
- Is Tema Pitagoras Relevant Today?
- Mathematical Proofs and Derivations
- Connections Between Pythagoras and Music
- How Did Pythagoras Influence Modern Math?
- Frequently Asked Questions
- Conclusion
Biography of Pythagoras
Pythagoras of Samos, the name behind the "tema pitagoras," was an ancient Greek mathematician, philosopher, and the founder of the Pythagorean Brotherhood. Born around 570 BCE, he is most famously credited with the Pythagorean Theorem, a cornerstone of mathematics. His contributions extended far beyond numbers, influencing philosophy, astronomy, and even mysticism. Pythagoras believed in the interconnection of all things, often stating, "All is number."
While much of what we know about Pythagoras comes from secondary sources, his teachings laid the groundwork for Western philosophy and mathematics. His emphasis on rational thought and systematic problem-solving established a legacy that continues to inspire mathematicians and thinkers worldwide. Below is a quick overview of his personal details:
| Full Name | Pythagoras of Samos |
|---|---|
| Birth Year | Circa 570 BCE |
| Birthplace | Samos, Greece |
| Primary Contributions | Pythagorean Theorem, Philosophy, Astronomy |
| Famous Quote | "All is number." |
What Is the Tema Pitagoras?
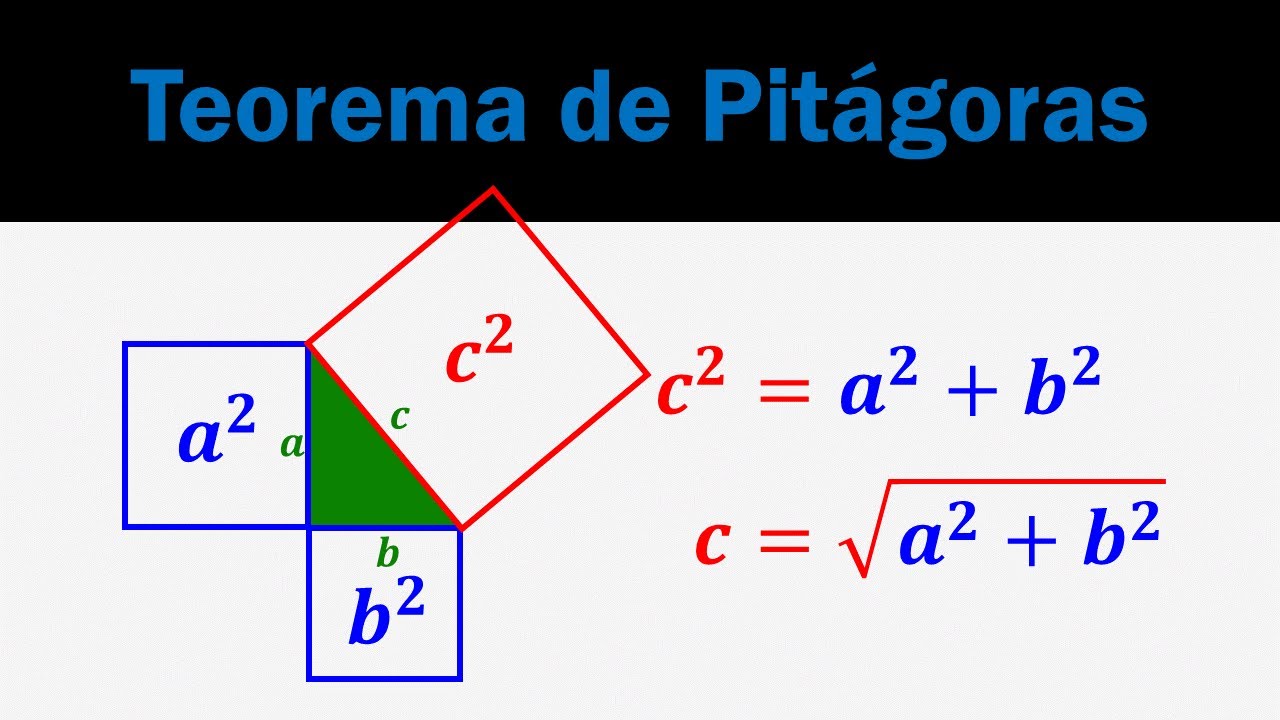
The "tema pitagoras" refers to the study and application of principles established by Pythagoras, particularly the Pythagorean Theorem. This theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Mathematically, it is expressed as:
a² + b² = c²
Though simple in its formulation, the theorem is profound in its implications. It has become a foundational concept in geometry and trigonometry, impacting everything from architectural design to navigation systems. The "tema pitagoras" also extends into other areas, such as number theory and musical harmony, showcasing the versatility of Pythagoras' teachings.
Historical Significance of Tema Pitagoras
The "tema pitagoras" has played a pivotal role in the history of mathematics. Originating in ancient Greece, it bridged the gap between abstract thought and practical application. Ancient civilizations like the Babylonians and Egyptians were already using principles similar to the Pythagorean Theorem long before Pythagoras formalized them.
Pythagoras' work also influenced other great thinkers, such as Plato and Euclid, who expanded on his ideas to develop comprehensive mathematical systems. The theorem's universality and timelessness underscore its historical importance, cementing its place in the annals of mathematics and science.
Key Principles of the Pythagorean Theorem
The Pythagorean Theorem is based on the relationship between the sides of a right-angled triangle. Its key principles include:
- Right-Angled Triangle: The theorem applies exclusively to triangles with a 90-degree angle.
- Hypotenuse: The side opposite the right angle, which is the longest side of the triangle.
- Legs: The two shorter sides of the triangle that form the right angle.
- Mathematical Relationship: The square of the hypotenuse is equal to the sum of the squares of the other two sides.
These principles form the core of the "tema pitagoras," enabling its wide-ranging applications in various fields.
How Does the Pythagorean Theorem Work?
To understand how the Pythagorean Theorem works, consider a right-angled triangle with sides of lengths a, b, and c (with c being the hypotenuse). According to the theorem:
a² + b² = c²
For example, if a triangle has sides of length 3 and 4, the hypotenuse can be calculated as follows:
3² + 4² = c²
9 + 16 = 25
c = √25 = 5
This simple yet powerful relationship demonstrates the theorem's utility in solving geometric problems.
Real-World Applications of Tema Pitagoras
The "tema pitagoras" has numerous real-world applications, including:
- Architecture: Designing buildings and structures.
- Navigation: Calculating distances and plotting routes.
- Physics: Analyzing forces and vectors.
- Engineering: Solving structural and mechanical problems.
Its versatility makes it an indispensable tool in both academic and practical contexts.
Article Recommendations
- Unveiling The Salt Trick For Penis Enlargement Myth Or Reality
- Unveiling The Details About Rudy Youngblood Wife A Comprehensive Insight
- Exploring Kannada Movierulzcom A Gateway To Kannada Cinema